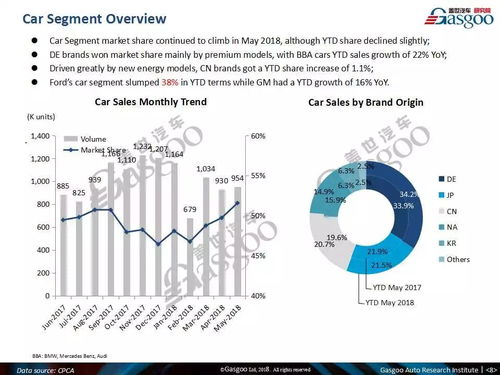
Introduction

The study of chaos theory has been a significant area of research in mathematics and physics, particularly in the context of nonlinear dynamical systems. Chen's system, proposed by Chinese mathematician Shangyou Chen in 1989, is a classic example of a chaotic system. This article aims to analyze the hyper-chaos generated from Chen's system, exploring its characteristics, generation mechanisms, and implications in various fields.
Background and Definition of Hyper-Chaos

Chen's system is a three-dimensional autonomous dynamical system defined by the following equations:
[ begin{align}
x' &= alpha x - yz,
y' &= xz - beta y,
z' &= xy - gamma z,
end{align} ]
where ( alpha, beta, gamma ) are system parameters. Hyper-chaos refers to a higher-dimensional chaotic behavior that exhibits more complex and unpredictable dynamics compared to standard chaos. In the case of Chen's system, hyper-chaos arises when the system is extended to a four-dimensional phase space.
Characteristics of Hyper-Chaos in Chen's System

The hyper-chaotic behavior in Chen's system can be characterized by several key features:
1. Sensitive Dependence on Initial Conditions: Hyper-chaos in Chen's system is highly sensitive to initial conditions, meaning that even tiny differences in starting values can lead to vastly different trajectories over time.
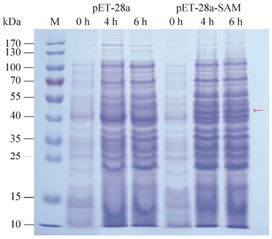
2. Complex Phase Space Structure: The four-dimensional phase space of the hyper-chaotic Chen system is characterized by a complex and intricate structure, with numerous attractors and strange attractors.

3. Nonlinear Dynamics: The system exhibits strong nonlinear interactions between its components, leading to the emergence of hyper-chaotic behavior.

4. Long-Term Memory: Despite its unpredictable nature, the hyper-chaotic Chen system can exhibit long-term memory effects, where past states influence future behavior.

Generation Mechanisms of Hyper-Chaos

The generation of hyper-chaos in Chen's system can be attributed to several factors:
1. Parameter Sensitivity: The system's parameters ( alpha, beta, gamma ) play a crucial role in determining the chaotic behavior. Small changes in these parameters can lead to the transition from regular to hyper-chaotic dynamics.

2. Nonlinear Interactions: The nonlinear interactions between the system's variables contribute to the complexity of the dynamics, making it difficult to predict the system's long-term behavior.

3. Attractor Bifurcation: The system undergoes a series of bifurcations, including period-doubling and torus breakdown, which lead to the emergence of hyper-chaotic attractors.

4. Fractal Dimensions: The fractal dimensions of the attractors in the hyper-chaotic Chen system are typically greater than 2, indicating the presence of complex and self-similar structures.

Applications and Implications
The hyper-chaotic behavior of Chen's system has significant implications in various fields:
1. Cryptography: The unpredictable nature of hyper-chaos makes it suitable for generating secure cryptographic keys, as the system's dynamics are difficult to predict and reproduce.

2. Physics: Hyper-chaos is relevant in the study of complex systems in physics, such as fluid dynamics and celestial mechanics, where chaotic behavior can lead to unpredictable outcomes.
4. Biology: The study of hyper-chaos can provide insights into the dynamics of biological systems, such as the heart's electrical activity and the behavior of neurons.
Conclusion
In conclusion, the hyper-chaos generated from Chen's system is a fascinating and complex phenomenon that exhibits unique characteristics and has wide-ranging implications. The analysis of this hyper-chaotic behavior provides valuable insights into the nature of chaos and its applications in various scientific and engineering disciplines. Further research into the generation mechanisms and control of hyper-chaos is likely to yield new discoveries and practical applications in the future.
















